GraphSAGE学习

1. 算法

链接：[1706.02216] Inductive Representation Learning on Large Graphs

概述

GraphSAGE是一个inductive的方法，在训练过程中，不会使用测试或者验证集的样本。而GCN在训练过程中，会采集测试或者验证集中的样本，因此为transductive

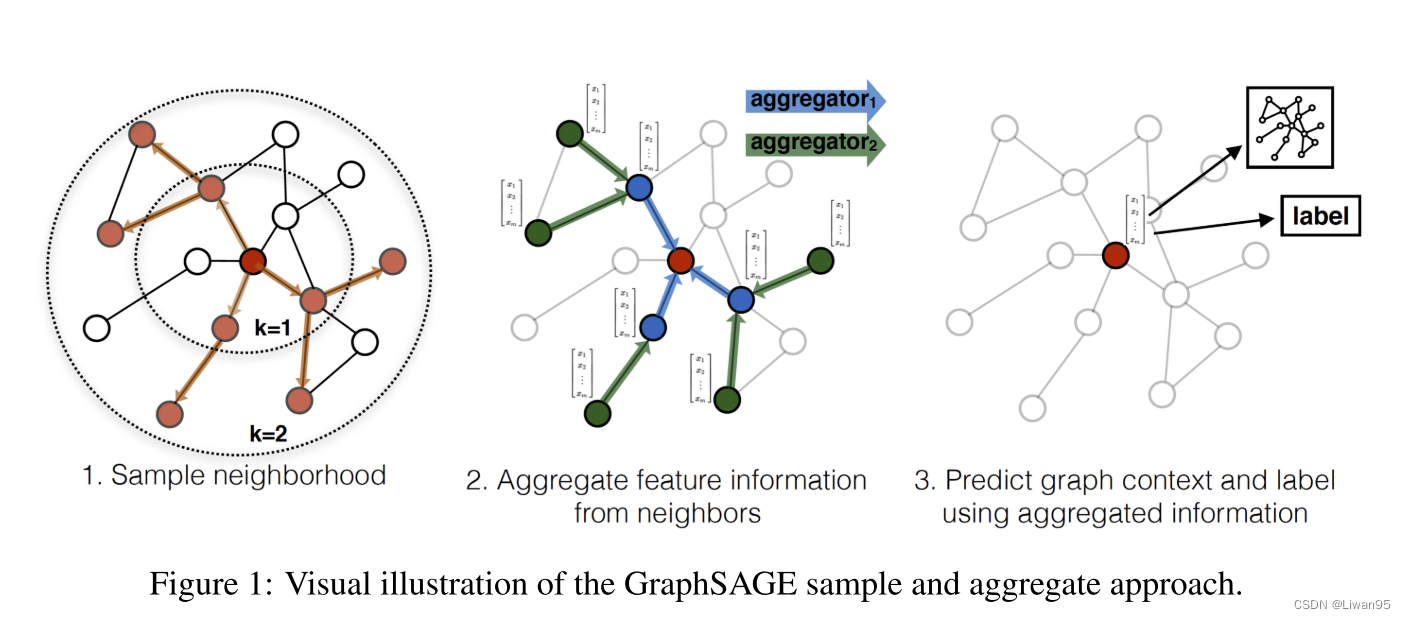
GraphSAGE

1. 对邻居采样
2. 采样后的邻居embedding传到节点上来，并使用一个聚合函数聚合这些邻居信息以更新节点的embedding
3. 根据更新后的embedding预测节点的标签

GraphSAGE采样和聚合流程示意图

嵌入向量生成（前向传播）算法

本节的内容假设模型已经完成训练，参数已经固定。

包括：

• 用来聚合节点邻居信息的$K$个聚合器$\mathrm{AGGREGATE}_k,\forall k\in{1,…,K}$

• 用来在不同的layer之间传播信息的$K$个权重矩阵$\mathbf{W}^{k},\forall k\in{1,…,K}$

下图详细描述了前向传播是如何进行的

1. 将每个节点的特征向量作为初始的Embedding
2. 对于每个节点，拿到它采样后的邻居的Embedding（$h_u, u \in \mathcal N(v)$）。并聚合邻居的Embedding。
   • $$\mathrm{h}_{\mathcal{N}(v)}^k\leftarrow\mathrm{AGGREGATE}_k({\mathbf{h}_u^{k-1},\forall u\in\mathcal{N}(v)})$$
3. 根据聚合后的邻居Embedding $\mathrm{h}_{\mathcal{N}(v)}^k$ 和节点自身的Embedding $h_v^{k-1}$，通过一个非线性变换更新自己的Embedding。
   • $$\mathbf{h}{v}^{k}\leftarrow\sigma\left(\mathbf{W}^{k}\cdot\text{coNcAT}(\mathbf{h}{v}^{k-1},\mathbf{h}_{\mathcal{N}(v)}^{k})\right)$$

文中的$K$, 既是聚合器的数量，也是权重矩阵的数量，还是网络的层数。

采样算法

GraphSAGE中的采样是定长的，通过事先定义的邻居个数S， 然后通过有放回的重采样/负采样方法。

从而保证：

• 可以把节点和他们的邻居拼成tensor送到GPU中训练

• 计算时每个批次的计算占用空间固定

• 使时间复杂度变得稳定，原本的时间复杂度可以达到$O(|\mathcal V|)$, 现在可以稳定$O(\prod_{i=1}^{K}S_{i}), i \in{1,…,K} $

学习GraphSAGE的参数

为了在完全无监督的图上进行学习，本文使用了一个基于图的损失函数，来调整$\mathbf{W}^{k}$和聚合器中的参数。

该损失函数鼓励邻近的节点具有相似的表示，并使不同的节点高度区分开。

$$J_{\mathcal{G}}(\mathbf{z}{u})=-\log\left(\sigma(\mathbf{z}{u}^{\top}\mathbf{z}{v})\right)-Q\cdot\mathbb{E}{v_{n}\sim P_{n}(v)}\log\left(\sigma(-\mathbf{z}{u}^{\top}\mathbf{z}{v_{n}})\right)$$

送入该损失函数的嵌入是通过节点的局部邻域中包含的特征生成的，而不是为每个节点生成一个唯一的嵌入。

如果是有监督的情况下，可以使用每个节点的预测lable和真实lable的交叉熵作为损失函数。

聚合器的结构

与规整的N-D形式不同，节点的邻居没有自然的顺序。因此，聚合函数必须要操作一个无序的向量集合。

在理想情况下，聚合器函数将是对称的，同时还是可训练的并且保持高的表示能力。

文章提出了三种候选的聚合器函数：

1. 平均聚合器：简单的取${\mathbf{h}_{u}^{k-1},\forall u\in\mathcal{N}(v)}$中每一个对应位置元素的均值
   • $$\mathbf{h}_v^k\leftarrow\sigma(\mathbf{W}\cdot\text{MEAN}({\mathbf{h}_v^{k-1}}\cup{\mathbf{h}_u^{k-1},\forall u\in\mathcal{N}(v)})$$
2. LSTM聚合器：与均值聚合器相比，LSTM具有更大的表达能力。但是，它不是对称的。
3. 池化聚合器：每个邻居的向量独立进入一个全连接神经网络，在经过这个变换之后，应用元素化最大池化操作来聚合跨邻居集合的信息。
   • $$\text{AGGREGATE}k^\text{pool}=\max(\left{\sigma\left(\mathbf{W}{\mathrm{pool}}\mathbf{h}_{u_i}^k+\mathbf{b}\right),\forall u_i\in\mathcal{N}(v)\right})$$

2. 总结

优点：

1. 使用采样机制，克服了GCN在训练时需要知道全部信息的问题，克服了对显存和内存的限制以及拓展性的问题。
2. 聚合器和权重矩阵的参数对于所有的节点是共享的
3. 模型的参数的数量与图的节点个数无关，这使得GraphSAGE能够处理更大的图
4. 既能处理有监督任务也能处理无监督任务

缺点：

在采样的时候没有考虑不同邻居的重要性

3. SAGEConv的实现

基于dgl和pytorch的sageconv的实现。包含了四种聚合器，以及对二分图和block同构图的处理。

此实现参考dgl官方的开源代码，链接在最下方。

import torch
from torch import nn
from torch.nn import functional as F
import dgl
from dgl import function as fn
from dgl.base import DGLError
from dgl.utils import expand_as_pair, check_eq_shape


class SAGEConv(nn.Module):
    def __init__(self,
                 in_feats,
                 out_feats,
                 aggregator_type,
                 feat_drop=0.0,
                 bias=True,
                 norm=None,
                 activation=None):
        super(SAGEConv, self).__init__()
        # 检查聚合器类型是否正确
        valid_aggregator_type = {'mean', 'gcn', 'pool', 'lstm'}
        if aggregator_type not in valid_aggregator_type:
            raise DGLError(
                "Invalid aggregator_type. Must be one of {}. "
                "But got {!r} instead.".format(
                    valid_aggregator_type, aggregator_type
                )
            )
        # 调用expand_as_pair，如果in_feats是tuple直接返回
        # 如果in_feats是int,则返回两相同此int值，分别代表源、目标节点特征维度
        self._in_src_feats, self._in_dst_feats = expand_as_pair(in_feats)
        self._out_feats = out_feats
        self._aggregator_type = aggregator_type
        self.norm = norm
        self.feat_drop = nn.Dropout(feat_drop)
        self.activation = activation

        # 创建聚合器函数
        if aggregator_type == "pool":
            self.fc_pool = nn.Linear(self._in_src_feats, self._in_src_feats)
        if aggregator_type == 'lstm':
            self.lstm = nn.LSTM(self._in_src_feats, self._in_src_feats, batch_first=True)

        self.fc_neigh = nn.Linear(self._in_src_feats, out_feats, bias=False)

        if aggregator_type != 'gcn':
            self.fc_self = nn.Linear(self._in_dst_feats, out_feats, bias=bias)
        elif bias:
            self.bias = nn.parameter.Parameter(torch.zeros(self._out_feats))
        else:
            self.register_buffer('bias', None)

        self.reset_parameters()

    def reset_parameters(self):
        """Reinitialize learnable parameters."""
        gain = nn.init.calculate_gain('relu')
        if self._aggregator_type == 'pool':
            nn.init.xavier_uniform_(self.fc_pool.weight, gain=gain)
        if self._aggregator_type == 'lstm':
            self.lstm.reset_parameters()
        if self._aggregator_type != 'gcn':
            nn.init.xavier_uniform_(self.fc_self.weight, gain=gain)
        nn.init.xavier_uniform_(self.fc_neigh.weight, gain=gain)

    def _lstm_reducer(self, nodes):
        """
        实现一个LSTM聚合器
        :param nodes: 邻居节点
        :return:
        """
        # m形状为（B, L, D）
        # B : batch_size
        # L : num of neighbors
        # D : dims of features
        m = nodes.mailbox["m"]
        batch_size = m.shape[0]
        h = (
            m.new_zeros((1, batch_size, self._in_src_feats)),
            m.new_zeros((1, batch_size, self._in_src_feats))
        )
        _, (rst, _) = self.lstm(m, h)
        # rst形状为（B, D）
        return {"neigh": rst.squeeze(0)}

    def forward(self, graph, feat, edge_weight=None):
        """
        Compute GraphSAGE Layer
        :param graph: 图
        :param feat: 特征 （N, D_in）或 二分图（N_in, D_in_src）(N_out, D_out_src)
        :param edge_weight: 边权
        :return: 本层输出的特征（N_dst, D_out）
        """
        with graph.local_scope():
            # 判断输入的feat是哪一种
            if isinstance(feat, tuple):  # 单二分图
                feat_src = self.feat_drop(feat[0])
                feat_dst = self.feat_drop(feat[1])
            else:
                feat_src = feat_dst = self.feat_drop(feat)  # 同构图
                # 同构图的block情况
                if graph.is_block:
                    feat_dst = feat_src[:graph.number_of_dst_nodes()]

            # 定义一个消息传播函数
            msg_fn = fn.copy_u("h", 'm')

            # 如果有边权，则调用内置u_mul_e，把起点的h特征乘以边权重，再将结果赋给边的m特征
            if edge_weight is not None:
                assert edge_weight.shape[0] == graph.num_edges()
                graph.edata["_edge_weight"] = edge_weight
                msg_fn = fn.u_mul_e("h", "_edge_weight", "m")

            # 记录目标节点的原始特征
            h_self = feat_dst

            # 处理无边图的情况
            if graph.num_edges() == 0:
                graph.dstdata['neigh'] = torch.zeros(
                    feat_dst.shape[0], self._in_src_feats
                ).to(feat_dst)

            # 确定在消息传播之前是否应用线性转换
            # 如果输入特征的维度大于输出特征的维度，需要先通过一个线性层转换维度
            lin_before_mp = self._in_src_feats > self._out_feats

            # 消息传播
            if self._aggregator_type == 'mean':
                # 将特征置于节点中的‘h’中
                # 如果需要降维, 使用fc_neigh
                graph.srcdata["h"] = (self.fc_neigh(feat_src) if lin_before_mp else feat_src)
                # 通过消息传播更新模型
                # 将h复制给m, 对邻居的m求均值，然后赋值给neigh
                graph.update_all(msg_fn, fn.mean('m', 'neigh'))
                h_neigh = graph.dstdata["neigh"]
                if not lin_before_mp:
                    h_neigh = self.fc_neigh(h_neigh)
            elif self._aggregator_type == 'gcn':
                # 检查源节点和目标节点的形状是否一直
                check_eq_shape(feat)
                graph.srcdata["h"] = (
                    self.fc_neigh(feat_src) if lin_before_mp else feat_src
                )
                # 是否为二分图
                if isinstance(feat, tuple):
                    graph.dstdata['h'] = (
                        self.fc_neigh(feat_dst) if lin_before_mp else feat_dst
                    )
                else:
                    if graph.is_block:  # 同构图block的情况
                        graph.dst_data["h"] = graph.srcdata["h"][:graph.num_dst_nodes()]
                    else:
                        graph.dstdata['h'] = graph.srcdata['h']
                # 将h复制到m, 然后把邻居节点的m聚合起来赋值为neigh
                graph.update_all(msg_fn, fn.sum("m", "neigh"))
                # 除以入度
                degs = graph.in_degrees().to(feat_dst)
                h_neigh = (graph.dstdata['neigh'] + graph.dstdata['h']) / (degs.unsqueeze(-1) + 1)
                if not lin_before_mp:
                    h_neigh = self.fc_neigh(h_neigh)
            elif self._aggregator_type == 'pool':
                # 将feat_src经过一个池化和激活函数放进h
                graph.srcdata['h'] = F.relu(self.fc_pool(feat_src))
                # h复制到m, 然后使用最大化聚合m和neigh
                graph.update_all(msg_fn, fn.max('m', 'neigh'))
                # 对聚合结果进行一个线性转化
                h_neigh = self.fc_neigh(graph.dstdata['neigh'])
            elif self._aggregator_type == "lstm":
                graph.srcdata["h"] = feat_src
                # 通过自己设置的lstm-reduce聚合
                graph.update_all(msg_fn, self._lstm_reducer)
                h_neigh = self.fc_neigh(graph.dstdata["neigh"])
            else:
                raise KeyError(
                    "Aggregator type {} not recognized.".format(
                        self._aggre_type
                    )
                )

            # GraphSAGE GCN 不需要fc_self
            if self._aggregator_type == 'gcn':
                rst = h_neigh
                # 手动为GCN添加偏置
                if self.bias is not None:
                    rst = rst + self.bias
            else:
                rst = self.fc_self(h_self) + h_neigh

            # 激活函数
            if self.activation is not None:
                rst = self.activation(rst)
            # 归一化
            if self.norm is not None:
                rst = self.norm(rst)
            return rst

4. 模型训练代码

训练模型代码：

可以选择在cora,citeseer,pubmed上训练，模型结构为包含两个gcn聚合的sageconv层。

结果：

* cora: ~0.8330
* citeseer: ~0.7110
* pubmed: ~0.7830

此代码为全图训练

import argparse

import dgl
import torch
from torch import nn
import torch.nn.functional as F
from sageconv import SAGEConv
from dgl import AddSelfLoop
from dgl.data import CiteseerGraphDataset, CoraGraphDataset, PubmedGraphDataset


class SAGE(nn.Module):
    def __init__(self, in_size, hid_size, out_size):
        super().__init__()
        self.layers = nn.ModuleList()
        # 一个两层的SAGE
        self.layers.append(SAGEConv(in_size, hid_size, 'gcn'))
        self.layers.append(SAGEConv(hid_size, out_size, 'gcn'))
        self.dropout = nn.Dropout(0.5)

    def forward(self, graph, x):
        h = self.dropout(x)
        for i, layer in enumerate(self.layers):
            h = layer(graph, h)
            if i != len(self.layers) - 1:
                h = F.relu(h)
                h = self.dropout(h)
        return h


def evaluate(g, features, labels, mask, model):
    model.eval()
    with torch.no_grad():
        logits = model(g, features)
        logits = logits[mask]
        labels = labels[mask]
        _, indices = torch.max(logits, dim=1)
        correct = torch.sum(indices == labels)
        return correct.item() * 1.0 / len(labels)


def train(g, features, labels, masks, model):
    # 划分训练集/验证集，损失函数和优化器
    train_mask, val_mask = masks
    loss_fcn = nn.CrossEntropyLoss()
    optimizer = torch.optim.Adam(model.parameters(),
                                 lr=1e-2,
                                 weight_decay=5e-4)
    # train loop
    for epoch in range(1, 201):
        model.train()
        logits = model(g, features)
        loss = loss_fcn(logits[train_mask], labels[train_mask])
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        acc = evaluate(g, features, labels, val_mask, model)
        print(
            "Epoch {:05d} | Loss {:.4f} | Accuracy {:.4f} ".format(
                epoch, loss.item(), acc
            )
        )


if __name__ == "__main__":
    parser = argparse.ArgumentParser(description="GraphSAGE")
    parser.add_argument(
        "--dataset",
        type=str,
        default='cora',
        help="Dataset name ('cora', 'citeseer', 'pubmed')",
    )
    parser.add_argument(
        "--dt",
        type=str,
        default="float",
        help="data type(float, bfloat16)",
    )
    args = parser.parse_args()
    print("Training with GraphSAGE module based on dgl")
    # load and preprocess dataset
    transform = (
        AddSelfLoop()
    )  # by default, it will first remove self-loops to prevent duplication
    if args.dataset == "cora":
        data = CoraGraphDataset(transform=transform)
    elif args.dataset == "citeseer":
        data = CiteseerGraphDataset(transform=transform)
    elif args.dataset == "pubmed":
        data = PubmedGraphDataset(transform=transform)
    else:
        raise ValueError("Unknown dataset: {}".format(args.dataset))
    g = data[0]
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    g = g.int().to(device)
    features = g.ndata["feat"]
    labels = g.ndata["label"]
    masks = g.ndata["train_mask"], g.ndata["val_mask"]

    # create GraphSAGE model
    in_size = features.shape[1]
    out_size = data.num_classes
    model = SAGE(in_size, 16, out_size).to(device)

    # convert model and graph to bfloat16 if needed
    if args.dt == "bfloat16":
        g = dgl.to_bfloat16(g)
        features = features.to(dtype=torch.bfloat16)
        model = model.to(dtype=torch.bfloat16)

    # model training
    print("Training...")
    train(g, features, labels, masks, model)

    # test the model
    print("Testing...")
    acc = evaluate(g, features, labels, g.ndata["test_mask"], model)
    print("Test accuracy {:.4f}".format(acc))

4. 参考链接

GNN 教程：GraphSAGE - ArchWalker

图神经网络从入门到入门 - 知乎 (zhihu.com)

dgl.nn.pytorch.conv.sageconv — DGL 1.1.1 documentation

dgl的官方示例