HAN学习

[TOC]

论文思路

摘要

本文首先提出了一种新的基于分层注意力的异构图神经网络，包括节点级和语义级的注意力。具体来说，节点级注意力旨在学习节点与其基于元路径的邻居之间的重要性，而语义级注意力能够学习不同元路径的重要性。通过学习节点级和语义级注意力的重要性，可以充分考虑节点和元路径的重要性。然后，所提出的模型可以以分层的方式通过基于源路径的邻居节点聚合特征来生成节点嵌入。

HAN模型

HAN模型使用分层的注意力结构：分为节点级别的注意力和语义级别的注意力。

节点级别：学习基于元路径的邻居的权重并聚合它们得到语义特定的节点嵌入。

语义级别：判断元路径的不同，并针对特定任务得到语义特定节点嵌入的最优加权组合。

下图为HAN的整体结构图。

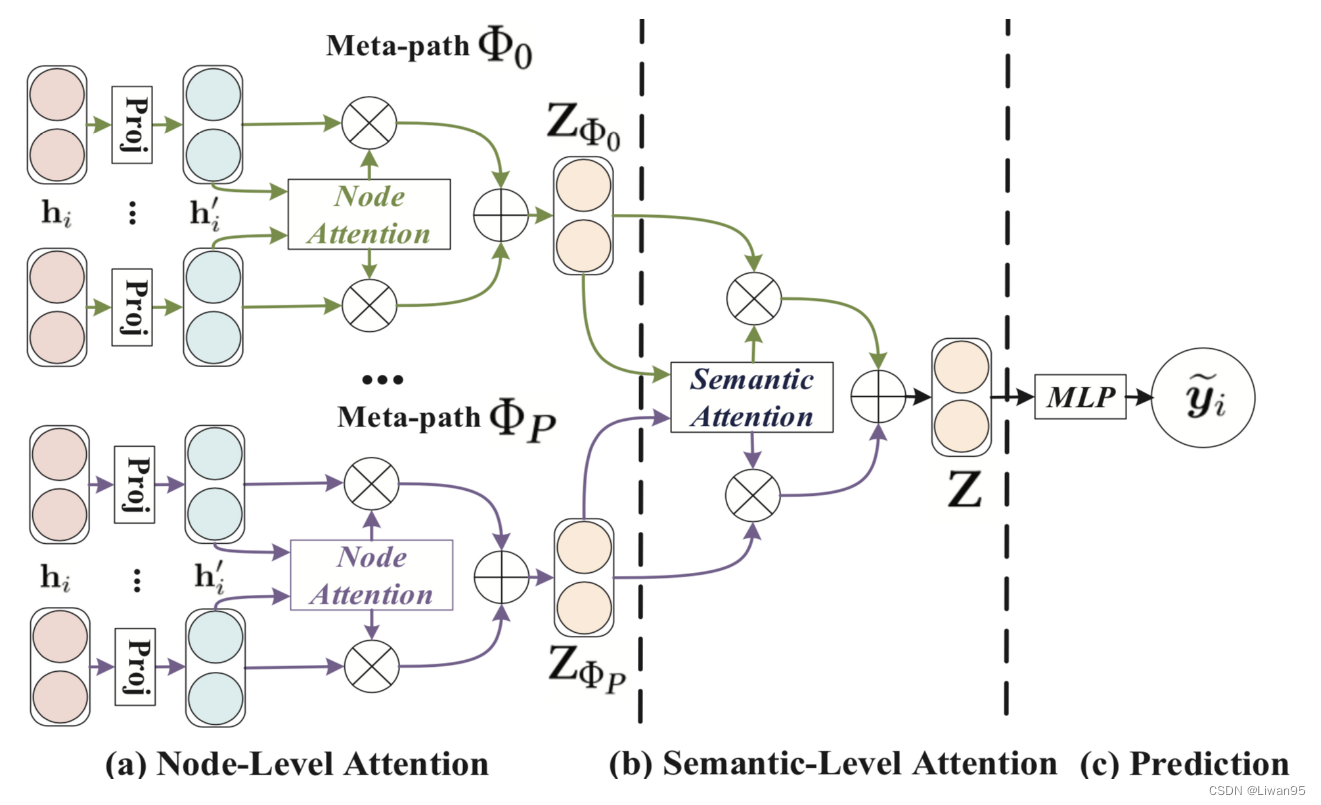
节点级别的注意力

由于每个类型的节点具有不同类型的特征，于是本文设计了类型特定的**转换矩阵$M_{\phi_{i}}$**将不同类型的节点特征映射到同一个特征空间中。映射过程如下公式1：

$$\mathbf{h}i^{\prime}=\mathbf{M}{\phi_i}\cdot\mathbf{h}_i $$

• $\mathbf{h}i$ 和 $\mathbf{h}{i}^{\prime}$ 分别为节点 $i$ 的原始特征和映射后的特征
• 经过映射之后，节点级别的注意力机制可以处理任意类型的节点。

接着，本文使用自我注意力学习各种类型节点的权重，给定一个节点对$(i,j)$ ，他们是通过元路径 $\Phi$，$e_{ij}^{\Phi}$代表节点$j$对节点$i$的重要性。如下公式2

$$e_{ij}^{\Phi}=att_{node}(\mathbf{h}_i^{\prime},\mathbf{h}_j^{\prime};\Phi)$$

• 这里的$att_{node}$表示执行节点级注意力的深度神经网络
• 对于指定的$\Phi$, $att_{node}$是共享的
• $e_{ij}^{\Phi}$ 不是对称的

然后，通过隐蔽注意力将结构信息注入模型（只需要对 $j\in\mathcal{N}{i}^{\Phi}$ 计算 $e{ij}^{\Phi}$）,$$\mathcal{N}_{i}^{\Phi}$$代表节点$i$基于元路径的邻居（包括自己），然后通过softmax函数进行**归一化得到重要性系数$\alpha_{ij}^{\Phi}$**。如下公式3

$$\alpha_{ij}^{\Phi}=softmax_{j}(e_{ij}^{\Phi})=\frac{\exp(\sigma(\mathbf{a}{\Phi}^{\mathrm{T}}\cdot[\mathbf{h}{i}^{\prime}|\mathbf{h}{j}^{\prime}]))}{\sum{k\in\mathcal{N}{i}^{\Phi}}\exp(\sigma(\mathbf{a}{\Phi}^{\mathrm{T}}\cdot[\mathbf{h}{i}^{\prime}|\mathbf{h}{k}^{\prime}]))}$$

• $\sigma $ 代表激活函数， $||$ 代表级联
• $\mathbf{a}_{\Phi}$ 是元路径$\Phi$对应的节点级别注意力向量

然后，节点$i$的基于元路径的嵌入可以通过邻居的映射后的特征根据重要性系数进行聚合决定。如下公式4

$$\mathbf{z}i^\Phi=\sigma\bigg(\sum{j\in\mathcal{N}i^\Phi}\alpha{ij}^\Phi\cdot\mathbf{h}_j’\bigg)$$

• $\mathbf{z}_i^\Phi$ 就是学习到的嵌入向量

由于异构图具有无标度特性，因此图数据的方差很大。为了解决上述挑战，我们将节点级注意力扩展到多头注意力，使训练过程更加稳定。如下公式5

$$\mathbf{z}{i}^{\Phi}=\prod\limits{k=1}^{K}\sigma\bigg(\sum\limits_{j\in\mathcal{N}{i}^{\Phi}}\alpha{ij}^{\Phi}\cdot\mathbf{h}_{j}’\bigg)$$

对于元路径集${\Phi_{1},\ldots,\Phi_{P}}$， 在节点的特征经过节点级别注意力之后，我们可以得到$P$组语义特定的节点特征，为$$\left{\mathbf{Z}{\Phi{1}},\ldots,\mathbf{Z}{\Phi{P}}\right}$$

语义级别的注意力

异构图中的每个节点通常包含多种类型的语义信息，语义特定的节点嵌入只能从一个方面反映节点。为了学习一个更全面的节点嵌入，我们需要融合多种语义，这些语义可以通过元路径来揭示。为了应对异构图中的元路径选择和语义融合挑战，作者提出了一种新颖的语义级注意力机制，用于自动学习不同元路径的重要性，并将它们融合到特定任务中。

将节点级注意力得到的$P$组语义特定的节点嵌入作为输入，每个元路径的权重可以被描述如下公式6：

$$(\beta_{\Phi_1},\ldots,\beta_{\Phi_P})=att_{sem}(\mathrm{Z}{\Phi_1},\ldots,\mathrm{Z}{\Phi_P})$$

为了学习每个元路径的重要性，首先通过非线性变换（例如，单层MLP）变换语义特定的嵌入向量

然后，我们通过变换嵌入与语义级注意向量$\mathbf q$的相似性度量语义特定嵌入的重要性。此外，对所有语义特定节点嵌入的重要性进行平均，这可以解释为每个元路径的重要性。如下公式7

$$w_{\Phi_{p}}=\frac{1}{|\mathcal{V}|}\sum_{i\in\mathcal{V}}\mathbf{q}^{\mathrm{T}}\cdot\tanh(\mathbf{W}\cdot\mathbf{z}{i}^{\Phi{p}}+\mathbf{b})$$

• $\mathbf W$是权重矩阵，$\mathbf b$是偏置向量，$\mathbf q$是语义级别的注意力向量
• 上边的参数都是所有元路径共享的

在得到每个元路径的重要性后，通过softmax函数对它们进行归一化。如下公式8

$$\beta_{\Phi_p}=\frac{\exp(w_{\Phi_p})}{\sum_{p=1}^{P}\exp(w_{\Phi_p})}$$

• 这可以解释为每个元路径在特定任务中的贡献

使用学习的权重作为系数，我们可以融合这些语义特定的嵌入以获得最终的嵌入。如下公式9

$$Z=\sum_{p=1}^{P}\beta_{\Phi_{p}}\cdot Z_{\Phi_{p}}$$

然后，我们可以将最终的嵌入应用于特定的任务，并设计不同的损失函数。

比如，对于半监督的节点分类任务，可以使用交叉熵损失函数。如下公式10

$$L=-\sum\limits_{l\in\mathcal{Y}_{L}}\mathrm{Y}^{l}\ln(\mathrm{C}\cdot\mathrm{Z}^{l})$$

节点级别的注意力和语义级别的注意力聚合过程图示：

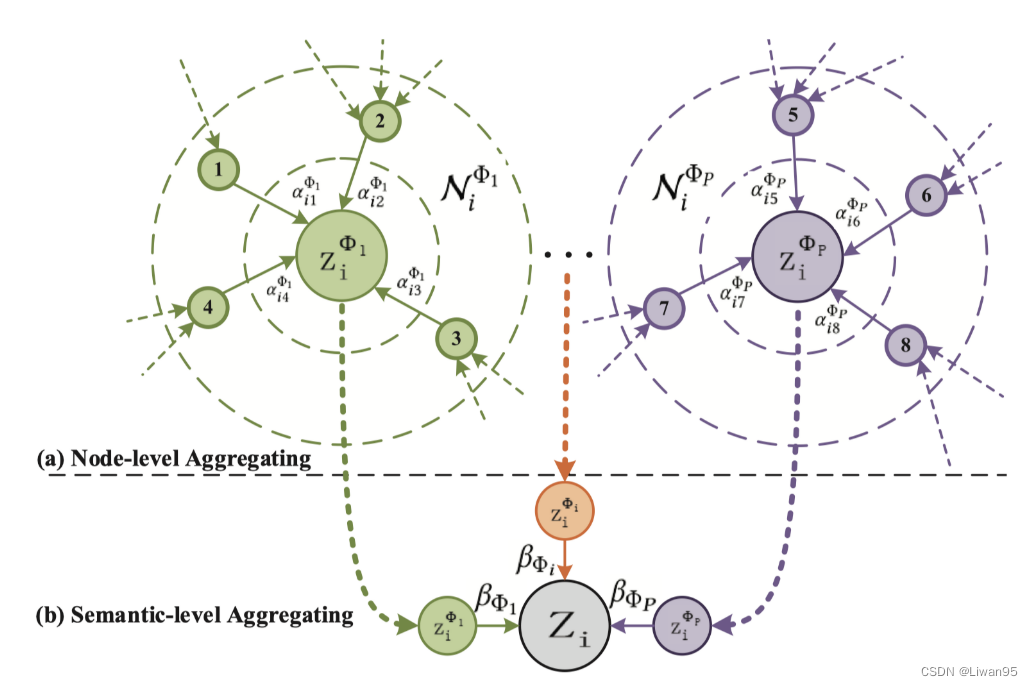
HAN的整个过程：

代码实现

此模型具体的实现有两种方式：主要区别在于对数据集的处理以及基于元路径邻居的获取。

• 直接读取作者处理过的数据集, 可以直接获取基于不同元路径的图

• dgl可以通过metapath_reachable_graph方法从一个异质图以及给定的元路径获取源路径的可达图

实现的具体思路相同，下边以第二种方式为例，给出代码（注释中详细解释了实现的思路和过程）:

下列代码中用到的其他工具类可以在Github仓库中找到

import dgl
import torch
import torch.nn as nn
import torch.nn.functional as F

from dgl.nn.pytorch import GATConv


"""
注释中的字母代表的含义：
N : 节点数量
M : 元路径数量
D : 嵌入向量维度
K : 多头注意力总数
"""


class SemanticAttention(nn.Module):
    def __init__(self, in_size, hidden_size=128):
        super(SemanticAttention, self).__init__()

        # 语义层次的注意力
        # 对应论文公式（7），最终得到每条元路径的重要性权重
        self.projection = nn.Sequential(
            nn.Linear(in_size, hidden_size),
            nn.Tanh(),
            nn.Linear(hidden_size, 1, bias=False)
        )

    def forward(self, z):
        # 输入的z为(N, M, K*D)
        # 经过映射之后的w形状为 (M , 1)
        w = self.projection(z).mean(0)
        # beta (M ,1)
        beta = torch.softmax(w, dim=0)
        # beta (N, M, 1)
        beta = beta.expand((z.shape[0],) + beta.shape)
        # (N, D*K)
        return (beta * z).sum(1)


class HANLayer(nn.Module):
    """
    meta_paths : list of metapaths, each as a list of edge types
    in_size : input feature dimension
    out_size : output feature dimension
    layer_num_heads : number of attention heads
    dropout : Dropout probability
    """

    def __init__(self,
                 meta_paths,
                 in_size,
                 out_size,
                 layer_num_heads,
                 drop_out):
        super(HANLayer, self).__init__()
        self.gat_layers = nn.ModuleList()

        for i in range(len(meta_paths)):
            # 使用GAT对应的GATConv层，完成节点层面的注意力
            # 之所以能够之间使用GATConv,是因为在forward中生成了每个元路径对应的可达图
            # 那么在进行节点级注意力的时候，节点的所有邻居都是它基于元路径的邻居
            # 节点级注意力以及聚合的过程就等同于GATConv的过程
            self.gat_layers.append(
                GATConv(
                    in_size,
                    out_size,
                    layer_num_heads,
                    drop_out,
                    drop_out,
                    activation=F.elu,
                    allow_zero_in_degree=True
                )
            )

            # 语义级注意力层
            self.semantic_attention = SemanticAttention(
                in_size=out_size * layer_num_heads
            )

            self.meta_paths = list(tuple(meta_path) for meta_path in meta_paths)

            # 缓存图
            self._cached_graph = None
            # 缓存每个元路径对应的可达图
            self._cached_coalesced_graph = {}

    def forward(self, g, h):
        semantic_embeddings = []

        if self._cached_graph is None or self._cached_graph is not g:
            self._cached_graph = g
            self._cached_coalesced_graph.clear()
            # 存储每个元路径对应的元路径可达图
            for meta_path in self.meta_paths:
                self._cached_coalesced_graph[
                    meta_path
                ] = dgl.metapath_reachable_graph(g, meta_path)

        for i, meta_path in enumerate(self.meta_paths):
            new_g = self._cached_coalesced_graph[meta_path]
            semantic_embeddings.append(self.gat_layers[i](new_g, h).flatten(1))
        # 经过对每个元路径进行节点级聚合
        # semantic_embeddings 为一个长度为M的列表
        # 其中的元素为每个节点级注意力的输出，形状为(N, D*K)

        # 将该列表在维度1堆叠，得到所有元路径的节点级注意力
        # 形状为(N, M, D * K)
        semantic_embeddings = torch.stack(
            semantic_embeddings, dim=1
        )

        # 最终经过语义级注意力聚合不同元路径的表示，得到了该层的输出
        # 形状为(N, D * K)
        return self.semantic_attention(semantic_embeddings)


class HAN(nn.Module):
    """
    参数：
    meta_paths : 元路径，使用边类型列表表示
    in_size : 输入大小（特征维度）
    out_size : 输出大小（节点种类数）
    num_heads : 多头注意力头数（列表形式，对应每层的头数）
    dropout : dropout概率
    """
    def __init__(
            self, meta_paths, in_size, hidden_size, out_size, num_heads, dropout
    ):
        super(HAN, self).__init__()

        self.layers = nn.ModuleList()
        # 第一个HAN层的输入输出需要单独定义
        self.layers.append(
            HANLayer(meta_paths, in_size, hidden_size, num_heads[0], dropout)
        )
        # 从第二个HAN层开始，每一个层的输入都是hidden_size * 上一个层的头数
        # 输出大小为 hidden_size * 当前层的头数
        for l in range(1, len(num_heads)):
            self.layers.append(
                HANLayer(
                    meta_paths,
                    hidden_size * num_heads[l - 1],
                    hidden_size,
                    num_heads[l],
                    dropout,
                )
            )
        # 最终的输出层
        self.predict = nn.Linear(hidden_size * num_heads[-1], out_size)

    def forward(self, g, h):
        for gnn in self.layers:
            h = gnn(g, h)

        return self.predict(h)