PathNet学习
PathNet
摘要
- GNN聚合函数的同质性假设限制了他们在异配图上的学习能力。
- 本文揭示了图中路径级别模式可以明确的反应丰富的语义和结构信息。
- 因此提出了一个新的结构感知路径聚合图神经网络(PathNet),以泛化GNN到同配和异配图。
- 首先,本文介绍了一个最大熵路径采样器,它可以帮助我们对包含结构上下文的多条路径进行采样。
- 然后,本文引入了一个结构感知的递归单元组成的顺序保持和距离感知组件学习的语义信息的邻域。
- 最后,对路径编码后不同路径对目标节点的偏好进行建模。
挑战
如何得到多个路径并编码正确的路径以获取足够的信息是极具挑战性的。
- 如何定义一个适当的采样器,可以避免过度膨胀的问题,同时保留有意义的结构信息
- 如何设计一个次序保持的聚合器。现有的GNN聚合器对Path中的order不敏感
- 如何捕捉路径对于不同节点的偏好
本文中,提出了一种 结构感知路径聚合图神经网络 来解决这些问题。
- 为了解决过度膨胀问题并保持结构,引入一个最大熵路径采样器
- 为了在保留高阶邻域上下文的同时对路径编码,引入一种结构感知路径编码器:具有以下优点
- 通过循环机制保留顺序
- 通过利用到目标结点的结构来捕获上下文
- 在路径编码之后,提出一种路径注意力机制模拟具有不同邻域同质性水平的节点的路径偏好。
PathNet
同配性和异配性:同质性的概念源于节点与其邻居具有相同类的倾向。
同质性程度可以通过同质性边比例来定量描述:$h(\mathcal{G})=\frac{|{(u,v){:}(u,v){\in}\mathcal{E}\wedge y_{u}=y_{v}}|}{|\mathcal{E}|}$
路径在表示图的复杂语义信息方面具有很大的潜力。
Maximal Entropy Path Sampler
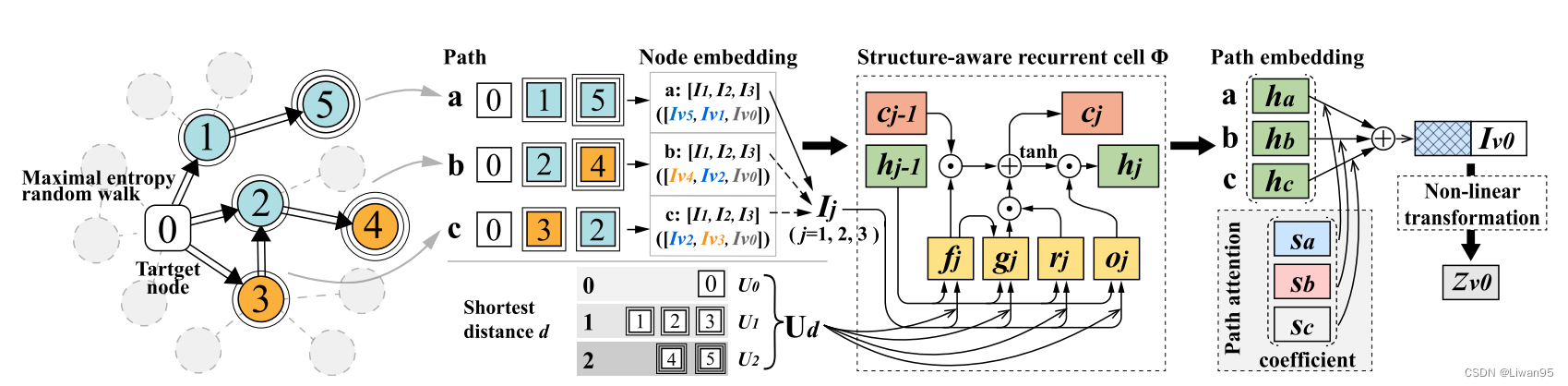
为了在考虑效率的情况下获得路径,需要像随机游走的采样策略。然而,传统的随机游走(CRW)的缺点是对不同的节点进行相同的处理,并且忽略了图中节点的中心性。为了解决这些问题,我们提出了在**最大熵随机游走(MERW)**的指导下对路径进行采样。
MERW算法在每一步搜索过程中都是沿着熵率增加的方向搜索路径,并引入了被广泛应用于衡量节点重要性的特征向量中心度。
图上随机游走的最大熵率 $\eta$ 可以从转移矩阵 $\mathcal{P}$ 和平稳分布 $\pi$ 计算,其可以描述如下:
$$\eta=-\sum_i\pi_i\sum_jp_{ij}\ln p_{ij} \quad(1)$$
- 随机游走的最大熵值有界于 $\text{ln}\lambda$ ,其中 $\lambda$ 是矩阵 $\text{A}$ 的最大特征值
为了最大化游走的熵率,MERW将转移概率构造为
$p_{ij} = \frac{A_{ij}u_j}{\lambda u_i}$
- $u=(u_{1},u_{2},\cdots,u_{n})$ 为归一化的特征向量
注意,转移概率与特征向量中心性成比例,从而保证MERW能够捕获图中节点的结构上下文。它可以被重新表示为最大熵转移(MET)矩阵,其被定义为
$$\mathbf{P}_u=\frac{\mathbf{D}_u^{-1}\mathbf{A}\mathbf{D}_u}{\lambda},\quad\quad\quad\quad\quad\quad(2)$$
- $$\mathbf{D}{u}=\mathrm{diag}(u{1},u_{2},\cdots,u_{n})$$
- 最大熵路径采样器不仅能最大化图的熵率,而且能获得图的复杂结构信息
结构感知路径聚合器
为了聚合路径信息,本文提出了一个结构感知路径聚合器。
具体来说,作者设计了一个结构化的递归单元来编码路径嵌入,它能够将路径中每个节点的顺序和距离信息结合起来,从而捕获语义信息。
此外,本文的路径偏好模型,区分不同的路径的重要性,实现自适应路径嵌入聚合。
结构感知循环单元
尽管传统GNN可以聚合高阶邻域的信息,但是它们由于使用同样的方式处理信息,并忽略了图中邻域的全局结构上下文,不可避免地导致了嵌入不可区分。
本文主张每个节点的距离是通过路径捕获结构上下文的关键信息。
本文提出了一个递归单元来编码路径序列,而不是独立地聚合每层节点,从而保留了每个节点的顺序信息。注意,在涉及结构信息之前,本文将所有节点特征 $\mathbf{X}$ 编码为节点嵌入 $\mathbf{I}$ ,其被描述为
$$\mathbf I=\sigma\left(\mathbf W_{\mathbf in}\mathbf X+\mathbf b_{\mathbf in}\right) \quad(3)$$
为了捕获基于特征的扩散结构,我们构造结构感知的递归单元 $\Phi $ 为
$$\begin{aligned}
&&\mathbf{r}{j}=\sigma\left(\mathbf{W}{\mathbf{r}}\cdot h_{j-1}+\mathbf{U}{\mathbf{d}}\cdot\mathbf{I}{j}\right), \
&&\mathbf{f}{j}=\sigma\left(\mathbf{W}{\mathbf{f}}\cdot h_{j-1}+\mathbf{U}{\mathbf{d}}\cdot\mathbf{I}{j}\right), \
&&\mathbf{o}{j}=\sigma\left(\mathbf{W{o}}\cdot h_{j-1}+\mathbf{U_{d}}\cdot\mathbf{I}{j}\right), \
&&\mathbf{g}{j}=\operatorname{tanh}\left(\mathbf{W}{\mathbf{g}}\cdot h{j-1}+\mathbf{U}{\mathbf{d}}\cdot\mathbf{I}{j}\right), \
&&\mathbf{c}{j}=\mathbf{f}{j}\odot\mathbf{c}{j-1}+\mathbf{r}{j}\odot\mathbf{g}{j}, \
&&\mathbf{h}{j}=\mathbf{o}{t}\odot\mathrm{tanh}\left(\mathbf{c}{j}\right), \
\end{aligned} \quad(4)$$
$\mathbf{h}_j$ 代表节点 $v$ 在路径中第 $j$ 步的表示
$\odot$ 是哈达玛积
考虑到目标节点的贡献最大,输入顺序与路径的收集顺序相反
考虑到距离信息对结构模式的贡献,采用了基于节点距离的参数共享机制的路径嵌入计算。具体地,对于路径中的每个节点,我们使用预先计算的距目标节点的最短距离 $d$ 作为辅助信息,并且具有相同 $d$ 的节点在路径编码期间共享相同的 $\mathbf{U}_d$ ,以便将距离信息并入路径嵌入。
建模路径偏好
自然的,具有不同同质度水平的邻域具有不同的路径偏好。对于同质性邻域,临近目标节点的路径对于分类贡献更多。然后对于异质性邻域,探索更广泛的图结构是更好的。
因此,我们为每个节点的路径偏好建模,即考虑不同的路径,并学习它们的重要性,以促进自适应嵌入聚合。
具体来说,对于一个特定的路径 $p$ ,我们可以得到它的嵌入 $h_p$ , 然后与目标节点的嵌入 $\mathbf{I}v$ 进行级联,作为通过可训练权重 $a$ 计算偏好系数 $s{v,p}$ 的输入
$$\boldsymbol{s}_{v,p}=\text{SOFTMAX}\left(\delta\left(\boldsymbol{a}\left(\mathbf{I}_v|\mathbf{h}_p\right)\right)\right)\quad(5)$$
$\delta$ 为 LeakyReLU
最后,使用偏好系数 $s_{v,p}$ 权衡路径并获取最终的预测 $z_v$
$$\mathbf{z}v=\sigma\left(\mathbf{W}{\mathbf{out}}\left(\mathbf{I}v|\sum_\limits{j\in p}s{v,p}\mathbf{h}p\right)+\mathbf{b}{\mathbf{out}}\right)\quad(6)$$
