When Do GNNs Work
When Do GNNs Work
摘要
- 现存的多种GNN模型中,包含的一个关键的部分是邻居聚合,其中每个节点的嵌入向量是通过参考它的邻居节点更新的。
- 本文旨在通过以下问题为这种机制提供一种更好的理解
- 邻居聚合是否总是必要和有用的?答案是否定的,在以下两个情况中,邻居聚合是无益的
- 当一个节点的邻居节点高度不相似
- 当一个节点的嵌入已经和它的邻居节点相似时
- 邻居聚合是否总是必要和有用的?答案是否定的,在以下两个情况中,邻居聚合是无益的
- 本文提出了一种新的度量方式,定量的衡量这两种情况并将他们融合进一个自适应层。
问题引入
已经有研究证明,过高的聚合程度将来自不同集群的节点混合在一起,并将这种现象称为“over-smoothing”
但是,他们没有都没有从局部考虑不同的聚集度。事实上,如果我们允许聚合度在节点之间变化,GNN的性能可以显著提高。
那么,现在的问题是,如何控制单个节点的聚合程度?
为了解决以上问题,本文分析出两种聚合无用的情况
- 如果中心节点的邻居的学习到的特征/标签不一致(高熵),则进一步聚合可能会损害性能;
- 当中心节点的学习到的特征/标签与其邻居几乎相同时,不需要进一步聚合。
本文设计了一个Adaptive-layer,在训练过程中,检查每个节点的邻居节点的学习到的标签,并通过作者设计的metric,衡量聚合该邻居是否有用,并只允许有益的节点进行聚合。
贡献
- 从局部的视角分析了邻域聚合的作用
- 提出了两个直观且有规则的度量方法定量的描述了邻域聚合没有帮助的两种情况
- 将度量标准融合进一种新的自适应层的设计中
分析
GNN更新函数一般包含以下操作:非线性,线性映射,邻域聚合
过多的聚合会导致过平滑的现象。避免性能恶化的关键在于防止社团间(具有不同类别标签的节点)之间的混合。由此提出了本文的第一种度量:neighborhood entropy
此外,不同的节点最佳的聚合度是不一样的,因此本文提出第二种度量:center-neighbor similarity
Neighborhood Entropy
邻域聚合利用了网络中的同质性效应,即连接的节点应该是相似的。
进一步,节点的邻居们应该彼此相似。当邻居不同意时,我们将此视为假设可能不成立并且聚合信息可能是噪声的警告。
为了衡量一个特定节点的邻域的差异,计算邻域熵如下:
$$Score_{etp}(u)=-\int_{\mathbb{X}}f^{\mathcal{N}(u)}(x)\cdot\log(f^{\mathcal{N}(u)}{(x)})dx, \quad(5)$$
- $\mathbb{X}$ 代表特征空间
- $f^{\mathcal{N}(u)}$ 为节点 $u$ 的邻居的特征的 概率密度函数(Probability Density Function)(PDF)
然而,由于PDF是每个邻居节点的狄拉克函数在高维空间的和,因此计算该微分熵是不可行的,并且不是非常有用的。
我们使用预测的标签来计算节点 $u$ 的邻居的标签分布并计算其离散熵:
$$\begin{aligned}
Score_{etp}(u)& =-\sum_{c\in C}P_{c}(u)\log(P_{c}(u)), \
&&\text{(6)} \
P_{c}(u)& =\frac{|{v\in\mathcal{N}(u)|y_v=c}|}{|\mathcal{N}(u)|},
\end{aligned}$$
- $C$ 是所有标签的类别集合
- $Score_{etp}(u)$ 更大的话,节点 $u$ 的邻居节点的区别就更大
Center-Neighbor Similarity
当节点的特征与邻居节点的特征已经足够相似时,邻域聚合操作可能是多余的。
本文使用 pointwise mutual information(PMI) 描述中心节点和他的邻居们的相似性。
$$PMI(u;\mathcal{N}(u))=\frac{P(\mathcal{N}(u)|u)}{P(\mathcal{N}(u))}$$
由于我们没有邻居特征的概率分布的先验知识,我们假设它遵循均匀分布,这使得${P(\mathcal{N}(u))}$是常数。然后,相似性定义如下:
$$Score_{sim}(u)=P(\mathcal{N}(u)|u)=\frac{1}{|\mathcal{N}(u)|}\sum_{v\in\mathcal{N}(u)}\frac{f_u^Tf_v}{\sum_{k\in V}f_u^Tf_k},\quad(7)$$
- $u$ 为中心节点
- $\mathcal{N}(u)$ 是节点 $u$ 的邻居集。
- $f(u)$ 是节点 $u$ 的特征,可能是输入特征,学习到的特征,或者是节点预测的标签。
相似的,我们可以使用独热编码预测标签以计算该指标
$$Score_{sim}(u)=\frac{|{v\in\mathcal{N}(u)|y_{v}=y_{u}}|}{|\mathcal{N}(u)|\cdot|{v\in V|y_{v}=y_{u}}|}.\quad(8)$$
- $Score_{sim}(u)$ 越大,节点$u$与他的邻居越相似
在这种情况下,我们可以比较邻域聚合之前和之后的性能,并表明预测结果几乎相同,如以下定理1中正式推导的。
Theorem 1
假设我们使用每个标签的预测概率分布 $h_u$ 来计算$Score_{sim}$。
如果对所有的 $u \in V$ , 有 $Score_{sim}(u)\geq\epsilon $ 。则邻域聚合前后的 2-norm 损失之差 $\Delta\mathcal{L}\leq\sqrt{2(1-\frac{\epsilon|V|}{|C|})}$
证明:
- $f_u$ 为节点 $u$ 的初始特征
- $l_u$ 是节点 $u$ 的真是独热标签向量
- $h_u$ 是节点 $u$ 初始的预测标签分布
聚合后的预测标签分布为:$\hat{h_{u}}=\frac{1}{|\mathcal{N}(u)+1|}\sum_{v\in\mathcal{N}(u)\bigcup{u}}h_{v}$
$$\because\langle h_{u},\hat{h}{u}\rangle\geq\langle h{u},\frac{\sum_{v\in\mathcal{N}(u)}h_{v}}{|\mathcal{N}(u)|}\rangle\geq\epsilon\sum_{u\in V}\langle h_{u},h_{v}\rangle,\forall u\in V$$
因为 $\hat{h}_{u}$ 包含了节点 $u$ 本身的信息, 因此$h_u$与$\hat{h}_u$的内积要比后边的大
由于 $\epsilon \leq \frac{1}{|\mathcal{N}_{u}|}$ , 后半个不等式成立
$$\therefore\sum_{u\in V}\langle h_{u},\hat{h_{u}}\rangle\geq\epsilon\langle\sum_{u\in V}h_{u},\sum_{u\in V}h_{u}\rangle\geq\epsilon\frac{|V|^{2}}{|C|}$$
$\langle\sum_{u\in V}h_{u},\sum_{u\in V}h_{u}\rangle \geq |V|^2\langle{h_{avg}},{h_{avg}}\rangle \geq \frac{|V|^2}{|C|}$
$$\begin{aligned}
&\Delta\mathcal{L}=\frac{1}{|V|}\sum_{u\in V}(||h_{u}-l_{u}||-||\hat{h_{u}}-l_{u}||) \
&\leq\frac{1}{|V|}\sum_{u\in V}||h_u-\hat{h_u}||\leq\frac{\sqrt{|V|}}{|V|}\sqrt{\sum_{u\in V}||h_u-\hat{h_u}||^2} \
&=\frac{\sqrt{|V|}}{|V|}\sqrt{\sum_{u\in V}||h_u||^2+\sum_{u\in V}||\hat{h_u}||^2-2\sum_{u\in V}\langle h_u,\hat{h_u}\rangle} \
&\leq\frac{\sqrt{|V|}}{|V|}\sqrt{2|V|-2\frac{\epsilon|V|^2}{|C|}}=\sqrt{2(1-\frac{\epsilon|V|}{|C|})}.
\end{aligned}$$
第一步推导根据范数的三角不等式
$\begin{align}&\frac{1}{|V|}\sum_{u\in V}(||h_{u}-l_{u}||-||\hat{h_{u}}-l_{u}||)\ &\leq \frac{1}{|V|}\sum_{u\in V}(||h_u|| + ||l_u|| - ||\hat{h}u|| - ||l_u||) \quad (两边之和大于第三边) \ &=\frac{1}{|V|}\sum{u\in V}(||h_u|| - ||\hat{h}u||)\ &\leq \frac{1}{|V|}\sum{u\in V}(||h_u - \hat{h}_u||) \quad(两边之差小于第三边) \end{align}$
$\begin{align} &||h_u - \hat{h}_u||^2 \&= ||h_u - \hat{h}_u|| \cdot ||h_u - \hat{h}u|| \& = ||h_u||^2 + ||\hat{h}u||^2 - 2 \langle h{u},\hat{h}{u}\rangle \end{align}$
模型
经过上述分析,本文提出了一个 自适应层, 允许节点在每一轮邻域聚合的时候做出独立的决定。最终,每个节点可能会经历不同的 聚合度。
具体来说,在每一层中应用门控函数,控制邻域信息的影响。它的值由$Score_{sim}$ 和 $Score_{etp}$ 决定。
与SGC的精神相似,本文去除了所有的非线性层。
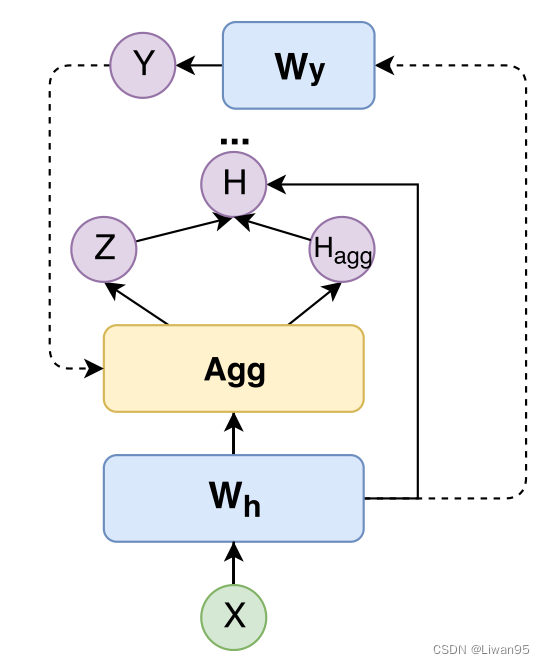
模型结构如下:
$$\begin{aligned}
h_{u}^{l+1}& =h_{u}^{l}+z_{l,u}Agg({h_{v}^{l}|v\in\mathcal{N}(u)}),\quad(1<l<L) \
h_{u}^{1}& =W_{h}Agg({x_{v}|v\in\mathcal{N}(u)}), \
y_{u}& =\mathrm{softmax}(W_{y}h_{u}^{L}),
\end{aligned} \quad(9)$$
- $z_{l,u}$ 是控制邻域聚合的随机变量
- 更新函数类似于残差层,原因如下:
- 残差层可以让模型堆叠更多的层
- 可以用同样的映射矩阵 $W_y$ 将隐藏状态 $h_u^l$ 映射到标签
使用以下公式计算门 $z_{l,u}$
$$z_{l,u}=\sigma(\tau_{1}-\mathrm{Norm}(Score_{sim}(l,u))) \cdot\sigma(\tau_{2}-\mathrm{Norm}(Score_{etp}(l,u))).
\quad(10)$$
激活函数 $\sigma$ 将 $z$ 值压缩到(0,1)
当$Score_{sim}$ 和 $Score_{etp}$ 都很大时,$z$ 会是一个接近0的数
$Norm$ 是批量归一化操作,用于重新缩放分数,以便它们在各层之间具有可比性。
为了简化,我们使用独热预测标签计算$Score_{sim}$ 和 $Score_{etp}$。 因为我们没有实际类大小的先验知识,我们假设所有的标签都具有相同的类大小。因此,标签类别大小项是常数,并且从计算中省略。
为了与基于注意力的方法比较,我们可以拓展模型以处理邻居的注意力权重。
$$\begin{aligned}
Score_{sim}^{att}(l,u)& =\sum_{v\in\mathcal{N}(u),y_{v}^{l}=y_{u}^{l}}a_{u,v}^{l}, \
Score_{etp}^{att}(l,u)& \begin{aligned}=-\sum_{y\in Y},P_{y}^{att}(l,u)\log(P_{y}^{att}(l,u))\quad(11)\end{aligned} \
P_{y}^{att}(l,u)& =\sum_{v\in\mathcal{N}(u),y_{v}^{l}=y}a_{u,v}^{l},
\end{aligned}$$
- $a_{u,v}^{l}$ 是节点 $u$ 对节点 $v$ 在 $l$ 层的注意力系数
我们还可以通过为每个注意力头部计算不同的 $z$ 来将我们的度量扩展到多头注意力,表示为$z^k_{l,u}$:
$$\begin{aligned}
h_{u}^{l+1}& =\mathop|\limits^K_{k=1}h_{u}^{l}+z_{l,u}^{k}Agg({h_{v}^{l}|v\in\mathcal{N}(u)})\quad(l<L-1), \
h_{u}^{L}& =\frac{1}{K}\sum_{k=1}^{K}(h_{u}^{L-1}+z_{L-1,u}^{k}Agg({h_{v}^{L-1}|v\in\mathcal{N}(u)})). \
&&\text{2)}
\end{aligned}$$
ALaGCN model