SUGRL
Simple Unsupervised Graph Representation Learning(简单的无监督图表示学习)
摘要
本文提出一种简单的无监督图表示学习方法以实现有效且高效的对比学习。
具体来说,本文提出的多重损失探索了结构信息和邻域信息之间的互补信息以增大类间差异,同时增加上限损失以实现正嵌入和锚嵌入之间的有限距离以减少类内差异。
此外,本文的方法从以前的图对比学习方法中删除了广泛使用的数据增强和鉴别器,同时可以输出低维嵌入,产生一个有效的模型。
贡献
- 首先,为了保证算法的有效性,提出了联合考虑结构信息和邻域信息来挖掘它们的互补信息,目的是扩大类间变异,以及设计一个上限损失来实现小的类内变异
- 其次,为了提高效率,我们将数据增强和鉴别器从对比学习中删除。这使得本文的方法很容易在大规模数据集上实现可扩展性。
- 最后,通过对8个公共基准数据集的综合实证研究,与11种比较方法进行了比较,验证了本文方法在节点分类方面的有效性和效率
方法
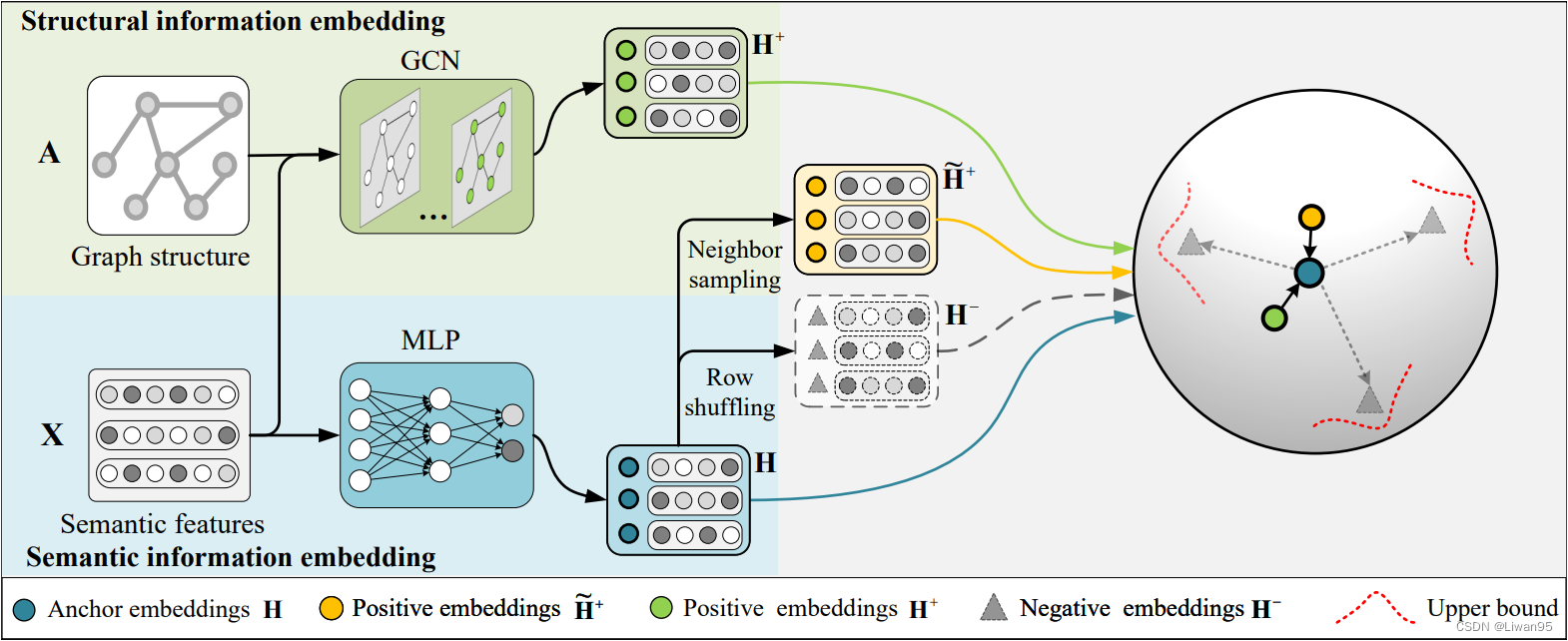
SUGRL侧重于MI最大化。在文献中,考虑到MI最大化的计算成本,SUGRL中的MI最大化被转移到对比学习,其中涉及锚嵌入,正嵌入和负嵌入,以及对比损失的定义。
Anchor and Negative Embedding Generation
现有的工作通常将节点表示或图形摘要视为锚点。
本文对于输入特征 $X$ 使用一个MLP以生成带有语义信息的 anchor embedding
$$\mathbf{X}^{(l+1)}=Dropout\left(\sigma\left(\mathbf{X}^{(l)}\mathbf{W}^{(l)}\right)\right)$$
$$\mathbf{H}=\mathbf{X}^{(l+1)}\mathbf{W}^{(l+1)}$$
- $X^{(0)} = X$
- $\sigma$ 是激活函数
- $\mathbf{W}^{(l)}$ 是第 $l$ 层的权重
对于负嵌入的生成,流行的方法(例如,DGI、GIC和MVGRL)是从原始图中获得损坏的图,然后用GCN对其进行处理。相比之下,本文直接对锚嵌入进行行混洗得到负嵌入,进一步减少了训练时间。
$$\mathbf{H}^-=\textit{Shuffle }([\mathbf{h}_1,\mathbf{h}_2,\ldots,\mathbf{h}_N])$$
总之,本文提出的方法通过去除GCN,减少了计算成本的同时保持了有效性。
Positive Embedding Generation
现存的工作大多将结构信息视作正嵌入。此外,以往的工作通常采用数据增强来获得不同的信息,以进行有效的对比学习,
相比之下,在本文中我们提出通过生成两种正嵌入来获得不同的信息,即,结构嵌入和邻域嵌入。具体来说,我们采用GCN和邻居采样方法来生成它们。
Structural information
为了得到图的结构信息,我们使用广泛使用的GCN作为基本编码器。
$$\mathbf{H}^{+^{(l+1)}}=\sigma\left(\widehat{\mathbf{A}}\mathbf{H}^{+^{(l)}}\mathbf{W}^{(l)}\right)$$
- $\mathbf{H}^{+(0)}=\mathbf{X}$ 且 $\mathbf{H}^{+(l)}$意味着第l层的特征
- $\widehat{\mathbf{A}}=\hat{\mathbf{D}}^{-1/2}\tilde{\mathbf{A}}\hat{\mathbf{D}}^{-1/2}\in\mathbb{R}^{N\times N}$ 是对称规范化邻接矩阵
- $\hat{\mathbf{D}}\in\mathbb{R}^{N\times N}$ 是 $\tilde{\mathbf{A}}={\mathbf{A}}+{\mathbf{I}}_N$ 的度矩阵。${\mathbf{I}}_N$ 是单位矩阵
值得注意的是,本文的方法直接共享了MLP和GCN编码器的权重(例如 $\mathbf{W}^{(l)}$),以进一步减少时间消耗。
Neighbor information
为了获得带有邻域信息的正嵌入,本文首先存储所有节点的邻居嵌入索引,然后进行采样,接着计算样本的平均值。这样可以高效的获取节点的邻域信息。
$$\widetilde{\mathbf{h}}i^+=\frac1m\sum{j=1}^m\left{\mathbf{h}_j\mid v_j\in\mathcal{N}_i\right}$$
总之,结构嵌入和邻居嵌入分别关注所有邻居和部分邻居。也就是说,结构嵌入代表一般表示,而邻居嵌入是特定表示。因此,他们从不同的角度解释样本,将它们一起考虑,以尽可能获得它们的互补信息。
Multiplet Loss
给定锚嵌入、正嵌入和负嵌入,对比学习旨在进行正对(即,锚和正嵌入)接近,同时保持负对(即,锚和负嵌入)相距很远。许多对比学习方法(例如,DGI、GMI、MVGRL和GIC)设计鉴别器(例如,双线性层)来区分正对和负对,但是鉴别器是耗时的。此外,减少泛化误差对于UGRL也很重要,因为训练过程中的小泛化误差可能会提高对比学习的泛化能力。此外,无论是减小类内变异还是扩大类间变异,都已被证明是减小泛化误差的有效方法
在SUGRL中,我们考虑的三重损失为基础,并设计一个上限损失,以从本文的方法中移除鉴别器(为了提高效率),并减少类内的差异,以及扩大类间的差异(为了提高有效性)。具体地,相对于每个采样的三重态损失可以公式化为:
$$\alpha+d\left(\mathbf{h},\mathbf{h}^+\right)<d\left(\mathbf{h},\mathbf{h}^-\right)$$
- $d(\cdot)$ 是一个相似度度量(例如:$\ell_2$范数距离)
- $\alpha$ 是一个非负值,以确保正嵌入和负嵌入之间的“安全”距离。
通过对所有负嵌入的损失求和,上式可以扩展到
$$\mathcal{L}{triplet}=\frac1k\sum{i=1}^k\left{d(\mathbf{h},\mathbf{h}^+\right)^2-d\left(\mathbf{h},\mathbf{h}i^-\right)^2+\alpha}+$$
- $${\cdot}_{+}=\max{\cdot,0}$$
- $k$ 是负样本的个数
为了增加类间的变异,我们应该把负对推得远离正对。为了实现这一点,我们采用了在上一节中定义的两种正嵌入上的三重损失,以得到:
$$\mathcal{L}S=\frac1k\sum{i=1}^k\left{d\left(\mathbf{h},\mathbf{h}^+\right)^2-d\left(\mathbf{h},\mathbf{h}i^-\right)^2+\alpha\right}+$$
$$\mathcal{L}N=\frac{1}{k}\sum{j=1}^k\left{d\left(\mathbf{h},\widetilde{\mathbf{h}}^+\right)^2-d\left(\mathbf{h},\mathbf{h}j^-\right)^2+\alpha\right}+$$
根据上一节的内容,结构嵌入($\mathrm{h^{+}}$)与邻域嵌入不同($\mathrm{\tilde{h}^{+}}$)。
根据两种类型的正嵌入与锚嵌入的距离不同,可以分为两种情况
Case 1: $$d\left(\mathbf{h},\mathbf{h}^{+}\right)^{2}\geq d(\mathbf{h},\widetilde{\mathbf{h}}^{+})^{2}$$
Case 2: $$d\left(\mathbf{h},\mathbf{h}^{+}\right)^{2}<d(\mathbf{h},\widetilde{\mathbf{h}}^{+})^{2}$$
如果是Case 1,在$\mathcal{L}_S$是0的情况是,$\mathcal{L}_N$一定是非0的。在这种情况下$\mathcal{L}_N$仍然是有效的,而$\mathcal{L}_S$是无效的。结果,负嵌入将继续远离锚嵌入,类间差异被放大。与Case 1类似,Case 2也可以扩大类间差异。
基于上述分析,Case 1或Case 2都可以扩大类间差异。特别是,如果其中一个是无效的,另一个仍然有效,以进一步扩大类间差异。因此,$\mathcal{L}_S$ 和 $\mathcal{L}_N$ 可以从结构嵌入和相邻嵌入中获得互补信息,从而能够放大类间的变异。
$\mathcal{L}_{triplet}$要求 $d\left(\mathbf{h},\mathbf{h}^{+}\right)^{2}$ 和 $d\left(\mathbf{h},\mathbf{h}i^-\right)^2$ 之间的距离应该大于$\alpha$,但它忽略了锚嵌入和正嵌入之间的距离。如果锚嵌入和正嵌入之间的距离大,则$\mathcal{L}{triplet}$中的{·}+项也可以是非零的。然而,在这种情况下,类内变化可能很大,不利于减少泛化误差。
为了解决这个问题,本文通过以下目标函数对于负对和正对研究了一个上限($\alpha + \beta$):
$$\alpha+d\left(\mathbf{h},\mathbf{h}^+\right)<d\left(\mathbf{h},\mathbf{h}^-\right)<d\left(\mathbf{h},\mathbf{h}^+\right)+\alpha+\beta $$
- $\beta$是一个非负微调参数
- 上界 $\alpha + \beta$ 保证了负嵌入和锚嵌入之间的距离是有限的,所以正嵌入和锚嵌入之间的距离也是有限的($$\alpha+d\left(\mathbf{h},\mathbf{h}^+\right)<d\left(\mathbf{h},\mathbf{h}^-\right)$$)
最终减少了类内差异。在对所有负嵌入的损失求和之后,所提出的减小类内变化的上限损失定义如下:
$$\mathcal{L}U=-\frac{1}{k}\sum{i=1}^k\left{d\left(\mathbf{h},\mathbf{h}^+\right)^2-d\left(\mathbf{h},\mathbf{h}i^-\right)^2+\alpha+\beta\right}-$$
- $${\cdot}_{-}=\min{\cdot,0}$$
值得注意的是,上界没有被应用于neighbor information。这是由于
- 每种信息都能达到相似的结果
- 在实验中同时使用它们并不能显着提高模型性能
最终,融合三重损失以及上界损失,本文提出的多重损失函数如下:
$$\mathcal{L}=\omega_1\mathcal{L}_S+\omega_2\mathcal{L}_N+\mathcal{L}_U$$
