GAT学习

论文内容

Graph Attention Networks

摘要：

本文提出了一种用在图结构数据上的新的神经网络结构。

此方法利用掩蔽的自注意层来解决基于图卷积或其近似的现有方法的缺点。

通过堆叠层，节点能够关注到他们的邻域的特征，允许（隐式地）为邻域中的不同节点指定不同的权重，而不需要任何昂贵的矩阵运算（例如求逆），也不需要事先知道图结构。

解决了邻域节点重要性不同的问题

图注意力层 Graph Attention Layer

GAL的输入是一组节点特征，$\mathbf{h}={\vec{h}{1},\vec{h}{2},\ldots,\vec{h}{N}},\vec{h}{i}\in\mathbb{R}^{F}$，其中$N$是节点的个数，$F$是每个节点的特征的个数。

输出：$$\mathbf{h}^{\prime}={\vec{h}{1}^{\prime},\vec{h}{2}^{\prime},\ldots,\vec{h}{N}^{\prime}},\vec{\vec{h}}{i}^{\prime}\in\mathbb{R}^{F^{\prime}}$$

计算过程

为了确保学习到足够的表达，至少需要一个线性转换将输入特征转换为更高级别的特征。最终，作为初始步骤，对于每个节点使用一个共享的线性表示，权重矩阵为$\mathbf{W}\in\mathbb{R}^{F^{\prime}\times F}$

然后对节点使用self-attention（一种共享注意力机制）$a:\mathbb{R}^{F^{‘}}\times\mathbb{R}^{F^{‘}}\to\mathbb{R}$计算注意力系数。

$e_{ij}=a(\mathbf{W}\vec{h}_i,\mathbf{W}\vec{h}_j)$这个公式代表节点$j$的特征对节点$i$的重要程度。本文只计算每个节点的一阶邻居节点对该节点的重要性。

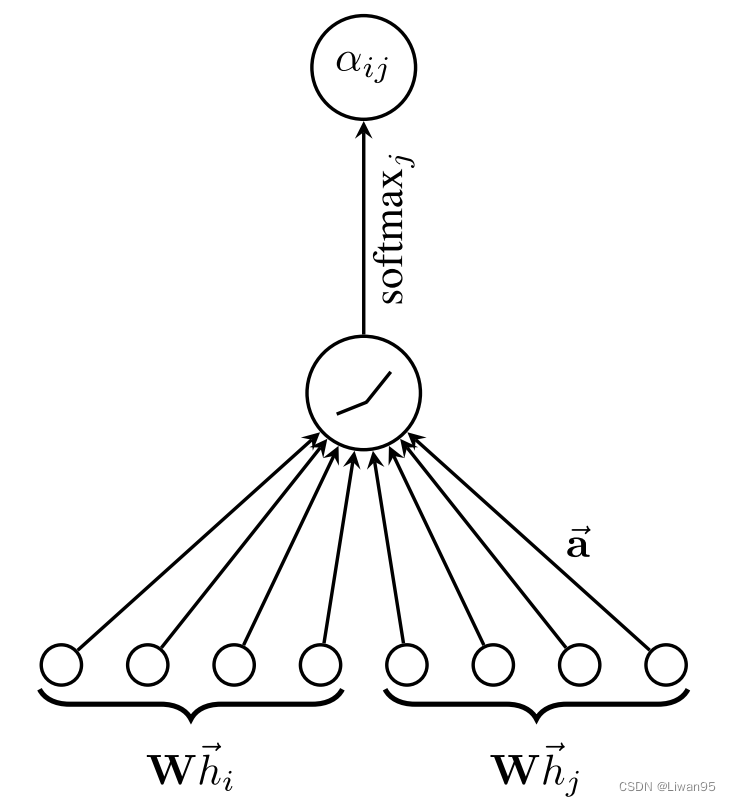
为了使这个重要性系数易于比较，本文使用softmax函数对他们进行归一化$\alpha_{ij}=\mathrm{softmax}j(e{ij})=\frac{\exp(e_{ij})}{\sum_{k\in\mathcal{N}i}\exp(e{ik})}$

注意力机制$a$是一个单层前向神经网络，权重向量为$\vec{\mathbf{a}}\in\mathbb{R}^{2F^{\prime}}$，并使用LeakyReLU非线性激活函数。

最终，结合上述的公式和内容，计算系数的公式如下

$$\alpha_{ij}=\frac{\exp\left(\text{LeakyReLU}\left(\vec{\mathbf{a}}^T[\textbf{W}\vec{h}_i|\textbf{W}\vec{h}j]\right)\right)}{\sum{k\in\mathcal{N}_i}\exp\left(\text{LeakyReLU}\left(\vec{\mathbf{a}}^T[\textbf{W}\vec{h}_i|\textbf{W}\vec{h}_k]\right)\right)}$$

其中节点i的向量为$\vec{h}_i$形状为$(F, 1)$, $\textbf{W}\vec{h}_i$ 形状为$(F^{\prime}, 1)$

将两个节点转换后的向量连在一起后形状为$(2F^{\prime}, 1 )$

与转置后的注意力向量$(1,2F^{\prime})$相乘得到重要性系数，最终通过激活函数和softmax归一化后得到最终的系数的值。

最终输出的向量为，每个邻居节点的注意力系数乘以对应节点经过线性变化得到的特征向量，全部加起来之后经过一个激活函数。公式如下：

$$\vec{h}i’=\sigma\left(\sum{j\in\mathcal{N}i}\alpha{ij}\mathbf{W}\vec{h}_j\right)$$

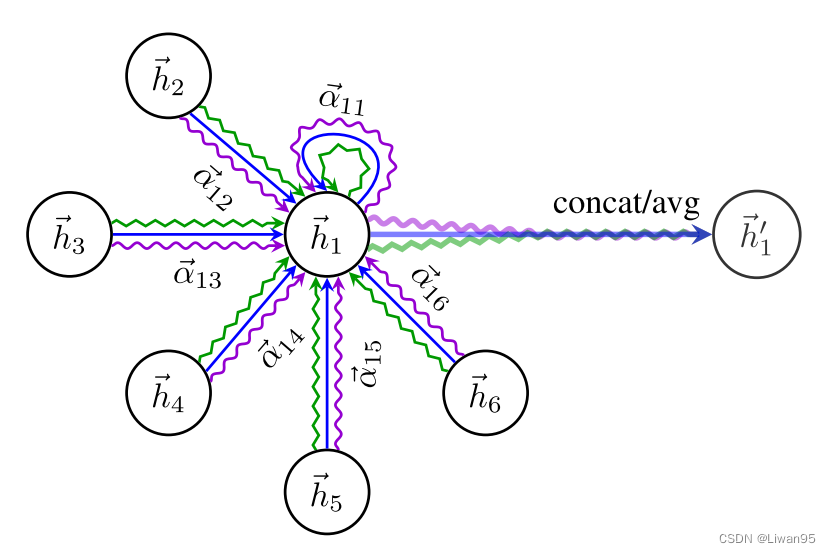
拓展注意力机制

为了稳定自我注意力机制的学习过程，作者发现通过使用多头注意力对于该机制是有益的。

具体来说，K个独立注意力机制执行上述的输出过程，然后它们的特征被级联，如下所示：

$$\vec{h}i’=\prod\limits{k=1}^K\sigma\left(\sum\limits_{j\in\mathcal{N}i}\alpha{ij}^k\mathbf{W}^k\vec{h}_j\right)$$

最终返回每个节点的$h^{\prime}$包含$KF^{\prime}$个特征。

注意，如果是最后一层，那么不应该级联，而应该求均值。

总结：

• GAT的效率很高，自注意力层的操作可以在所有的边上一起进行，输出特征的计算可以在所有节点上同时进行。不需要特征分解等消耗较大的矩阵运算。时间复杂度可以表示为$O(|V|{F}F^{\prime}{+}|E|F^{\prime})$，与GCN相当。
• 与GCN相比，GAT为同一个邻域中的节点分配了不同的重要性权重，从而使模型能力产生飞跃。
• 注意力机制以共享的方式应用于图中的所有边，并且因此它不依赖于对全局图结构或其所有节点的预先访问（许多现有技术的限制）。使GAT是inductive的。
• 相比于其他inductive的方法,GraphSAGE,取一个固定大小的邻域，这使GraphSAGE不能获取整个邻域。GAT不受此限制，它与整个邻域一起工作。
• 使用节点的特征进行相似性计算，而不是节点的结构属性。

未来工作的方向：

本文生成一个利用稀疏矩阵运算的GAT层版本，将节点和边的数量的存储复杂性降低到线性，并能够在更大的图形数据集上执行GAT模型。

然而，我们使用的张量操作框架仅支持秩为2的张量的稀疏矩阵乘法，这限制了该层当前实现的批处理能力（特别是对于具有多个图的数据集）。

妥善解决这一制约因素是今后工作的重要方向。取决于适当位置的图结构的规则性，在这些稀疏场景中，与CPU相比，GPU可能无法提供主要的性能优势。

还应该注意的是，模型的“感受野”的大小是由网络的深度上限（类似于GCN和类似模型）。诸如跳过连接的技术（Resnet）可以容易地应用于适当地延伸深度。最后，跨所有图边缘的并行化（特别是以分布式方式）可能涉及大量冗余计算，因为邻域通常在感兴趣的图中高度重叠。

实现

GATConv实现

GATConv实现（对于代码的理解都在注释中）

import torch
from torch import nn

import dgl.function as fn
from dgl.base import DGLError
from dgl.utils import expand_as_pair
from dgl.nn.functional import edge_softmax
from dgl.nn.pytorch.utils import Identity


class GATConv(nn.Module):
    def __init__(
            self,
            in_feats,
            out_feats,
            num_heads,
            feat_drop=0.0,
            attn_drop=0.0,
            negative_slope=0.2,
            residual=False,
            activation=None,
            allow_zero_in_degree=False,
            bias=True
    ):
        super(GATConv, self).__init__()
        self._num_heads = num_heads
        self._in_src_feats, self._in_dst_feats = expand_as_pair(in_feats)
        self._out_feats = out_feats
        self._allow_zero_in_degree = allow_zero_in_degree

        if isinstance(in_feats, tuple):
            # 二分图
            # 分别为两个特征创建一个线性转换层
            self.fc_src = nn.Linear(
                self._in_src_feats, out_feats * num_heads, bias=False
            )
            self.fc_dst = nn.Linear(
                self._in_dst_feats, out_feats * num_heads, bias=False
            )
        else:
            # 正常图直接创建一个线性转换层，相当于论文中的W
            self.fc = nn.Linear(
                self._in_src_feats, out_feats * num_heads, bias=False
            )

        # 创建注意力向量
        # dgl在实现时将源节点和目标节点的注意力分数，分开计算，因此有两个注意力向量
        # 详细的解释在forward()函数中
        self.attn_l = nn.Parameter(
            torch.FloatTensor(size=(1, num_heads, out_feats))
        )
        self.attn_r = nn.Parameter(
            torch.FloatTensor(size=(1, num_heads, out_feats))
        )

        # dropout层
        self.feat_drop = nn.Dropout(feat_drop)
        self.attn_drop = nn.Dropout(attn_drop)
        # 激活函数
        self.leaky_relu = nn.LeakyReLU(negative_slope)

        self.has_linear_res = False
        self.has_explicit_bias = False

        # 初始化多头自注意力层的参数，包括残差连接和偏置
        if residual:
            if self._in_dst_feats != out_feats * num_heads:
                self.res_fc = nn.Linear(
                    self._in_dst_feats, num_heads * out_feats, bias=bias
                )
                self.has_linear_res = True
            else:
                self.res_fc = Identity()
        else:
            self.register_buffer("res_fc", None)

        if bias and not self.has_linear_res:
            self.bias = nn.Parameter(torch.zeros(num_heads * out_feats, ))
            self.has_explicit_bias = True
        else:
            self.register_buffer("bias", None)

        self.reset_parameters()
        self.activation = activation

    def reset_parameters(self):
        """
        重新初始化可学习参数
        :return:
        """
        gain = nn.init.calculate_gain('relu')
        if hasattr(self, "fc"):
            nn.init.xavier_normal_(self.fc.weight, gain=gain)
        else:
            nn.init.xavier_normal_(self.fc_src.weight, gain=gain)
            nn.init.xavier_normal_(self.fc_dst.weight, gain=gain)

        nn.init.xavier_normal_(self.attn_l, gain=gain)
        nn.init.xavier_normal_(self.attn_r, gain=gain)

        if self.has_explicit_bias:
            nn.init.constant_(self.bias, 0)
        if isinstance(self.res_fc, nn.Linear):
            nn.init.xavier_normal_(self.res_fc.weight, gain=gain)
            if self.res_fc.bias is not None:
                nn.init.constant_(self.res_fc.bias, 0)

    def set_allow_zero_in_degree(self, set_value):
        """
        设置是否为0的标志
        :param set_value:
        :return:
        """
        self._allow_zero_in_degree = set_value

    def forward(self, graph, feat, edge_weight=None, get_attention=False):
        """
        前向传播
        :param graph: 图
        :param feat: 节点特征
        :param edge_weight: 边权
        :param get_attention: 是否返回注意力
        :return:
        """

        with graph.local_scope():
            if not self._allow_zero_in_degree:
                if (graph.in_degrees() == 0).any():
                    raise DGLError(
                        "There are 0-in-degree nodes in the graph, "
                        "output for those nodes will be invalid. "
                        "This is harmful for some applications, "
                        "causing silent performance regression. "
                        "Adding self-loop on the input graph by "
                        "calling `g = dgl.add_self_loop(g)` will resolve "
                        "the issue. Setting ``allow_zero_in_degree`` "
                        "to be `True` when constructing this module will "
                        "suppress the check and let the code run."
                    )

            # 该部分处理输入的特征，将特征经过线性转换后，存放在feat_src, feat_dst
            # 相当于 W h_i
            if isinstance(feat, tuple):
                # 二分图的情况
                src_prefix_shape = feat[0].shape[:-1]
                dst_prefix_shape = feat[1].shape[:-1]
                h_src = self.feat_drop(feat[0])
                h_dst = self.feat_drop(feat[1])

                if not hasattr(self, 'fc_src'):
                    feat_src = self.fc(h_src).view(
                        *src_prefix_shape, self._num_heads, self._out_feats
                    )
                    feat_dst = self.fc(h_dst).view(
                        *dst_prefix_shape, self._num_heads, self._out_feats
                    )
                else:
                    feat_src = self.fc_src(h_src).view(
                        *src_prefix_shape, self._num_heads, self._out_feats
                    )
                    feat_dst = self.fc_dst(h_dst).view(
                        *dst_prefix_shape, self._num_heads, self._out_feats
                    )

            else:
                # 同构图
                # 获取源节点和目标节点的个数
                src_prefix_shape = dst_prefix_shape = feat.shape[:-1]
                # 源节点和目标节点的特征（经过dropout）
                h_src = h_dst = self.feat_drop(feat)
                # 经过fc层后形状为(num_nodes, out_feats * num_heads)
                # 将形状变为(num_nodes, num_heads, out_feats)
                feat_src = feat_dst = self.fc(h_src).view(
                    *src_prefix_shape, self._num_heads, self._out_feats
                )
                # 对block的处理
                if graph.is_block:
                    feat_dst = feat_src[: graph.number_of_dst_nodes()]
                    h_dst = h_dst[: graph.number_of_dst_nodes()]
                    dst_prefix_shape = (
                                           graph.number_of_dst_nodes(),
                                       ) + dst_prefix_shape[1:]
            # NOTE: GAT paper uses "first concatenation then linear projection"
            # to compute attention scores, while ours is "first projection then
            # addition", the two approaches are mathematically equivalent:
            # We decompose the weight vector a mentioned in the paper into
            # [a_l || a_r], then
            # a^T [Wh_i || Wh_j] = a_l Wh_i + a_r Wh_j
            # Our implementation is much efficient because we do not need to
            # save [Wh_i || Wh_j] on edges, which is not memory-efficient. Plus,
            # addition could be optimized with DGL's built-in function u_add_v,
            # which further speeds up computation and saves memory footprint.

            # 计算注意力
            # 此部分对应论文中的公式（1）-（3）
            # (num_nodes, num_heads, out_feat) * (1, num_heads, out_feat)
            # 广播到形状一致后逐元素乘积, 将最后一个维度加起来，然后再添加一个维度
            # 最终el为(num_nodes, num_heads, 1)
            # 最后一个维度就是每个节点，每个注意力头对应的注意力分数
            # 这样完成了所有节点和所有注意力头同时计算
            el = (feat_src * self.attn_l).sum(dim=-1).unsqueeze(-1)
            # 目标节点计算注意力
            # 同上
            er = (feat_dst * self.attn_r).sum(dim=-1).unsqueeze(-1)

            # 将上边计算的特征和注意力值放入节点
            graph.srcdata.update({"ft": feat_src, "el": el})
            graph.dstdata.update({"er": er})

            # 计算每个边对应的注意力分数，将两个节点的分数加起来
            # 然后把值复制给边，这样每条边都对应一个注意力分数
            # compute edge attention, el and er are a_l Wh_i and a_r Wh_j respectively.
            graph.apply_edges(fn.u_add_v("el", "er", "e"))

            # 激活函数
            e = self.leaky_relu(graph.edata.pop("e"))

            # 为了使权重归一化，使用edge_softmax
            # compute softmax
            # 最终将每个边对应的注意力分数放入'a'
            # 计算结果形状为(num_edges, num_heads, 1)
            graph.edata["a"] = self.attn_drop(edge_softmax(graph, e))
            # 如果边本身有权重
            if edge_weight is not None:
                # 将(num_edges, 1)处理为（num_edges, num_heads, 1）
                # 然后相乘
                graph.edata["a"] = graph.edata["a"] * edge_weight.tile(
                    1, self._num_heads, 1
                ).transpose(0, 2)

            # 最终的消息传递阶段，对应论文公式（4）或者（5）
            # 消息函数：将节点对应的的特征乘以对应的注意力分数，放入'm'，产生消息
            # 聚合函数：聚集节点每个邻边产生的‘m’，求和后放入'ft'
            # message passing
            graph.update_all(fn.u_mul_e("ft", "a", "m"), fn.sum("m", "ft"))
            rst = graph.dstdata["ft"]

            # residual
            # 残差
            if self.res_fc is not None:
                # 如果有残差
                # Use -1 rather than self._num_heads to handle broadcasting
                resval = self.res_fc(h_dst).view(
                    *dst_prefix_shape, -1, self._out_feats
                )
                # 进行残差连接
                rst = rst + resval

            # 显式的偏置
            # bias
            if self.has_explicit_bias:
                rst = rst + self.bias.view(
                    *((1,) * len(dst_prefix_shape)),
                    self._num_heads,
                    self._out_feats
                )
            # activation
            if self.activation:
                rst = self.activation(rst)

            if get_attention:
                return rst, graph.edata["a"]
            else:
                return rst

训练代码

import argparse
import time

from gatconv import GATConv

import torch
import torch.nn as nn
import torch.nn.functional as F
from dgl import AddSelfLoop
from dgl.data import CiteseerGraphDataset, CoraGraphDataset, PubmedGraphDataset


class GAT(nn.Module):
    def __init__(self, in_size, hid_size, out_size, heads):
        super().__init__()
        self.gat_layers = nn.ModuleList()
        # two-layer GAT
        self.gat_layers.append(
            GATConv(
                in_size,
                hid_size,
                heads[0],
                feat_drop=0.6,
                attn_drop=0.6,
                activation=F.elu,
            )
        )
        self.gat_layers.append(
            GATConv(
                hid_size * heads[0],
                out_size,
                heads[1],
                feat_drop=0.6,
                attn_drop=0.6,
                activation=None,
            )
        )

    def forward(self, g, inputs):
        h = inputs
        for i, layer in enumerate(self.gat_layers):
            h = layer(g, h)
            if i == len(self.gat_layers) - 1:  # last layer
                h = h.mean(1)
            else:  # other layer(s)
                h = h.flatten(1)
        return h


def evaluate(g, features, labels, mask, model):
    model.eval()
    with torch.no_grad():
        logits = model(g, features)
        logits = logits[mask]
        labels = labels[mask]
        _, indices = torch.max(logits, dim=1)
        correct = torch.sum(indices == labels)
        return correct.item() * 1.0 / len(labels)


def train(g, features, labels, masks, model, num_epochs):
    # Define train/val samples, loss function and optimizer
    train_mask = masks[0]
    val_mask = masks[1]
    loss_fcn = nn.CrossEntropyLoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=5e-3, weight_decay=5e-4)

    for epoch in range(num_epochs):
        t0 = time.time()
        model.train()
        logits = model(g, features)
        loss = loss_fcn(logits[train_mask], labels[train_mask])
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        acc = evaluate(g, features, labels, val_mask, model)
        t1 = time.time()
        print(
            "Epoch {:05d} | Loss {:.4f} | Accuracy {:.4f} | Time {:.4f}".format(
                epoch, loss.item(), acc, t1 - t0
            )
        )


if __name__ == "__main__":
    parser = argparse.ArgumentParser()
    parser.add_argument(
        "--dataset",
        type=str,
        default="cora",
        help="Dataset name ('cora', 'citeseer', 'pubmed').",
    )
    parser.add_argument(
        "--num_epochs",
        type=int,
        default=200,
        help="Number of epochs for train.",
    )
    parser.add_argument(
        "--num_gpus",
        type=int,
        default=0,
        help="Number of GPUs used for train and evaluation.",
    )
    args = parser.parse_args()
    print(f"Training with GATConv module.")

    # Load and preprocess dataset
    transform = (
        AddSelfLoop()
    )  # by default, it will first remove self-loops to prevent duplication
    if args.dataset == "cora":
        data = CoraGraphDataset(transform=transform)
    elif args.dataset == "citeseer":
        data = CiteseerGraphDataset(transform=transform)
    elif args.dataset == "pubmed":
        data = PubmedGraphDataset(transform=transform)
    else:
        raise ValueError("Unknown dataset: {}".format(args.dataset))
    g = data[0]
    if args.num_gpus > 0 and torch.cuda.is_available():
        device = torch.device("cuda")
    else:
        device = torch.device("cpu")
    g = g.int().to(device)
    features = g.ndata["feat"]
    labels = g.ndata["label"]
    masks = g.ndata["train_mask"], g.ndata["val_mask"], g.ndata["test_mask"]

    # Create GAT model
    in_size = features.shape[1]
    out_size = data.num_classes
    model = GAT(in_size, 8, out_size, heads=[8, 1]).to(device)

    print("Training...")
    train(g, features, labels, masks, model, args.num_epochs)

    print("Testing...")
    acc = evaluate(g, features, labels, masks[2], model)
    print("Test accuracy {:.4f}".format(acc))

参考链接

Graph Attention Networks

dgl/examples/core/gat/train.py

dgl/python/dgl/nn/pytorch/conv/gatconv.py